Guided Labeling 3: Model Uncertainty

In this series, we've have been exploring the topic of guided labeling by looking at active learning and label density. In the first episode we introduced the topic of active learning and active learning sampling and moved on to look at label density in the second article. Here are the links to the two previous episodes:

In this third episode, we are moving on to look at Model Uncertainty.

Using label density we explore the feature space and retrain the model each time with new labels that are both representative of a good subset of unlabeled data and different from already labeled data of past iterations. However, besides selecting data points based on the overall distribution, we should also prioritize missing labels based on the attached model predictions. In every iteration we can score the data that still need to be labeled with the retrained model. What can we infer given those predictions by the constantly re-trained model?

Before we can answer this question there is another common concept in machine learning classification related to the feature space: the decision boundary. The decision boundary defines a hyper-surface in the feature space of n dimensions, which separates data points depending on the predicted label. In Figure 1 we point again to our data set with only two columns: weight and height. In this case the decision boundary is a line drawn machine learning model to predict overweight and underweight conditions. In this example we use a line, however we could have also used a curve or a closed shape.

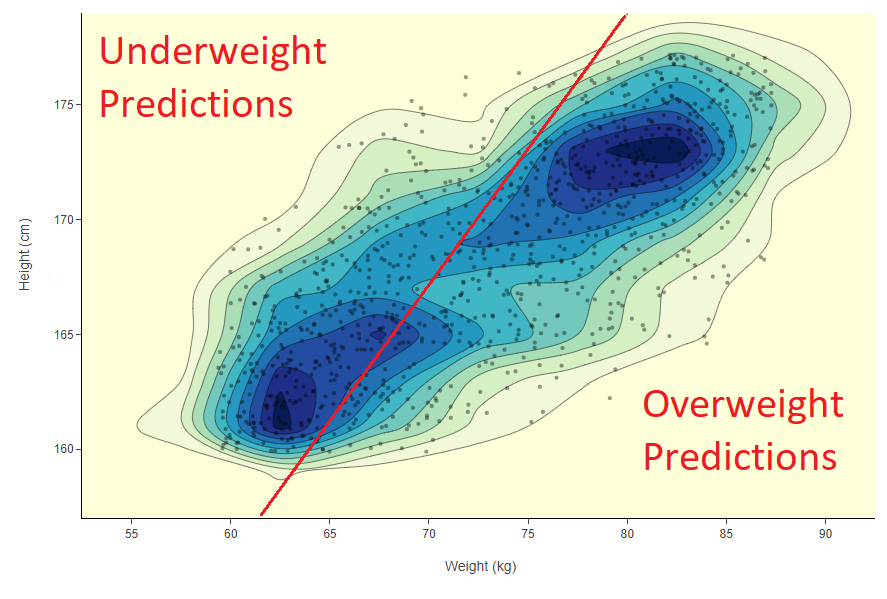
Fig. 1: In the 2D feature space of weight vs height we train a machine learning model to distinguish overweight and underweight subjects. The model prediction is visually and conceptually represented by the decision boundary - a line dividing the subjects in the two categories.

So let’s say we are training an SVM model - starting with no labels and using active learning. That is we are trying to find the right line. We label a few subjects in the beginning using label density. Subjects are labeled by simply applying an heuristics called body mass index - no need for a domain expert in this simple example.

In the beginning, the position of the decision boundary will probably be wrong as it is based on only a few data points in the most dense areas. However the more labels you keep adding the more the line will position itself closer to the actual separation between the two classes. Our focus here is to move this decision boundary to the right position using as few labels as possible. In active learning, this means using as little time as possible of our expensive human-in-the-loop expert.

To use less labels we need data points positioned around the decision boundary, as these are the data points best defining defining the line we are looking for. But how do we find them, not knowing where this decision boundary lies? The answer is, we use model predictions - and, to be more precise - we use model certainty.

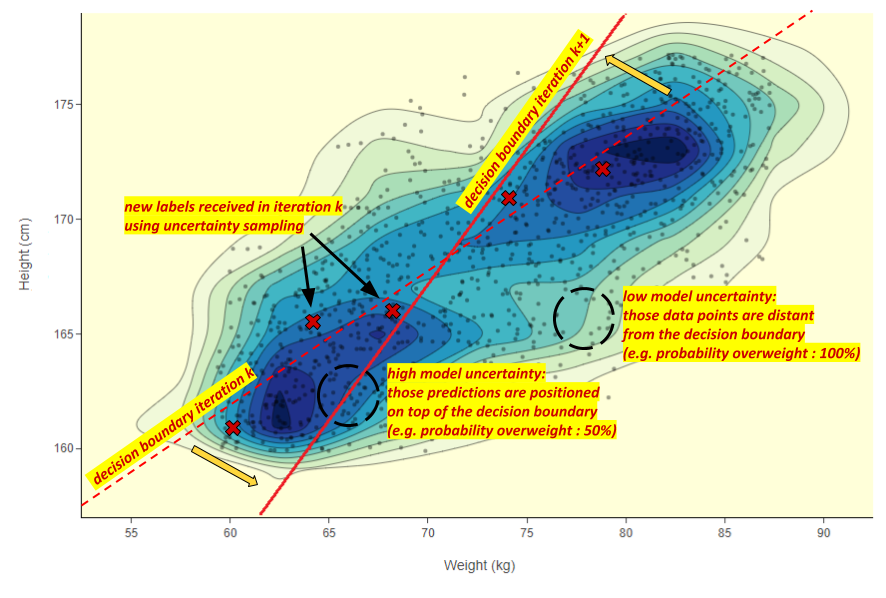
Fig. 2: In the 2D dimensional feature space, the dotted decision boundary belongs to the model trained in the current iteration k. To move the decision boundary in the right direction we use uncertainty sampling, asking the user to label new data points near to the current decision boundary. We then identify misclassification, which subsequently leads to a better decision boundary in the next iteration after the model is retrained.

Looking for misclassification using uncertainty

At each iteration the decision boundary moves when a new point is labeled contradicting the model prediction. The intuition behind model certainty is that a misclassification is more likely to happen when the model is uncertain of its prediction. When the model has already achieved decent performance, model uncertainty is symptomatic of misclassification being more probable, i.e. a wrong prediction. In the feature space, model uncertainty increases as you get closer to the decision boundary. To quickly move our decision boundary to the right position we therefore look for misclassification using uncertainty. In this manner, we select data points that are close to the actual decision boundary (Fig. 2).

So here we go: at each iteration we score all unlabeled data points with the re-trained model. Next, we compute the model uncertainty, take the top uncertain predictions and we ask the user to label them. By retraining the model with all of the corrected predictions we are likely to move the decision boundary in the right direction and achieve better performance with less labels.

How do we measure model certainty/uncertainty?

There are different metrics; we are going to use the entropy score (Form. 3). This is a concept common in information theory. High entropy is a symptom of high uncertainty. This strategy is also known as uncertainty sampling and you can find the details in the blog article Labeling with Active Learning, which was first published in Data Science Central.

Prediction Entropy Formula

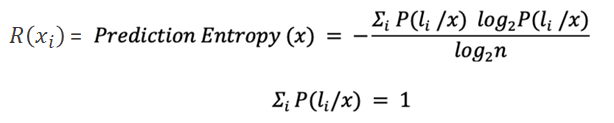
Given a prediction for row x by the classification model we can retrieve a probability vector P(l/x) which sums up to 1 and shows the different n probability of a row to belong to a possible target class l_i. Using such prediction vector we can measure its entropy score between 0 and 1 to define the uncertainty of the model in predicting P(l/x).

Wrapping up

In today's episode, we've taken a look at how model uncertainty can be used as a rapid way of moving our decision boundary to the correct position using as few labels as possible i.e. taking up as little time as possible of our expensive human-in-the-loop expert.

In the fourth episode of our Guided Labeling Blog Series we will go on to use uncertainty sampling to exploit the key areas of the feature space to an ensure an improvement of the decision boundary.

Stay tuned to our blog post channel for the next episode and also for more posts on other data science topics!

The Guided Labeling KNIME Blog Series

By Paolo Tamagnini and Adrian Nembach (KNIME)