An intrusion in network data, a sudden pathological status in medicine, a fraudulent payment in sales or credit card businesses, and, finally, a mechanical piece breakdown in machinery are all examples of unknown and often undesirable events, deviations from the “normal” behavior.
Predicting the unknown in different kinds of IoT data is well established by now, and a high value, in terms of money, life expectancy, and/or time, is usually associated with the early discovery. Yet it comes with challenges! In most cases, the available data are non-labeled, so we don’t know if the past signals were anomalous or normal. Therefore, we can only apply unsupervised models that predict unknown disruptive events based on the normal functioning only.
In the field of mechanical maintenance this is called “anomaly detection”. There is a lot of data that lends itself to unsupervised anomaly detection use cases: turbines, rotors, chemical reactions, medical signals, spectroscopy, and so on. In our case here, we deal with rotor data.
The goal of this “Anomaly Detection in Predictive Maintenance” series is to be able to predict a breakdown episode without any previous examples.
In this third and final part, we’ll approach this challenge with an auto-regressive model. Our analysis builds on the first and second parts of the series. In the first part we standardized and time aligned the FFT preprocessed sensor data, and explored its visual patterns. In the second part we predicted the rotor breakdown with a simple model called a Control Chart.
Today’s Approach: An Auto-Regressive Model
An auto-regressive model predicts time series values by a linear combination of its past values. It assumes that the time series shows auto-correlation; that the past value is correlated with the current value. The model will be able to predict the next sample in the time series, when the system works properly. The error between the reality sample and the predicted sample can then tell us something about the underlying system’s condition.
We train an auto-regressive model using the linear regression algorithm. The predictor columns contain past values of the target column: φ
yt = c+φ1yt-1 + φ2yt-2+...+φpyt-p + εt,
Where yt is the target column
yt-1, yt-2, ...,yt-p are the predictor columns i.e. past values of yt up to the lag p
φ1, φ2, ...,φ3 are the regression coefficients, and
εt is the white noise error term
In our example, we use p=10, which means that we consider 10 past values for each prediction. This parameter can also be optimized for a better prediction performance.
The Anomaly Detection. Time Series AR Training workflow in Figure 1 shows the model training process. Altogether we train 313 models, one for each different frequency band of the original time series. You can download the Anomaly Detection. Time Series AR Training workflow from the KNIME Hub.
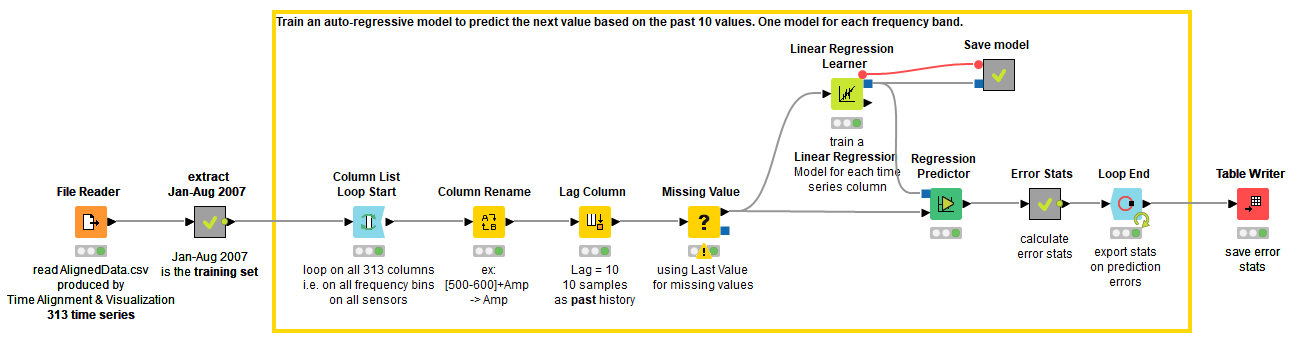
Train the Model
For model training we use the already preprocessed data as described in the first part of the series. The data include three time windows (training, maintenance and test), which are defined based on the date of the rotor breakdown, which is July 21, 2008:
- Training window from January to August 2007
- Maintenance window from September 2007 to July 21, 2008
- Test window after July 22, 2008
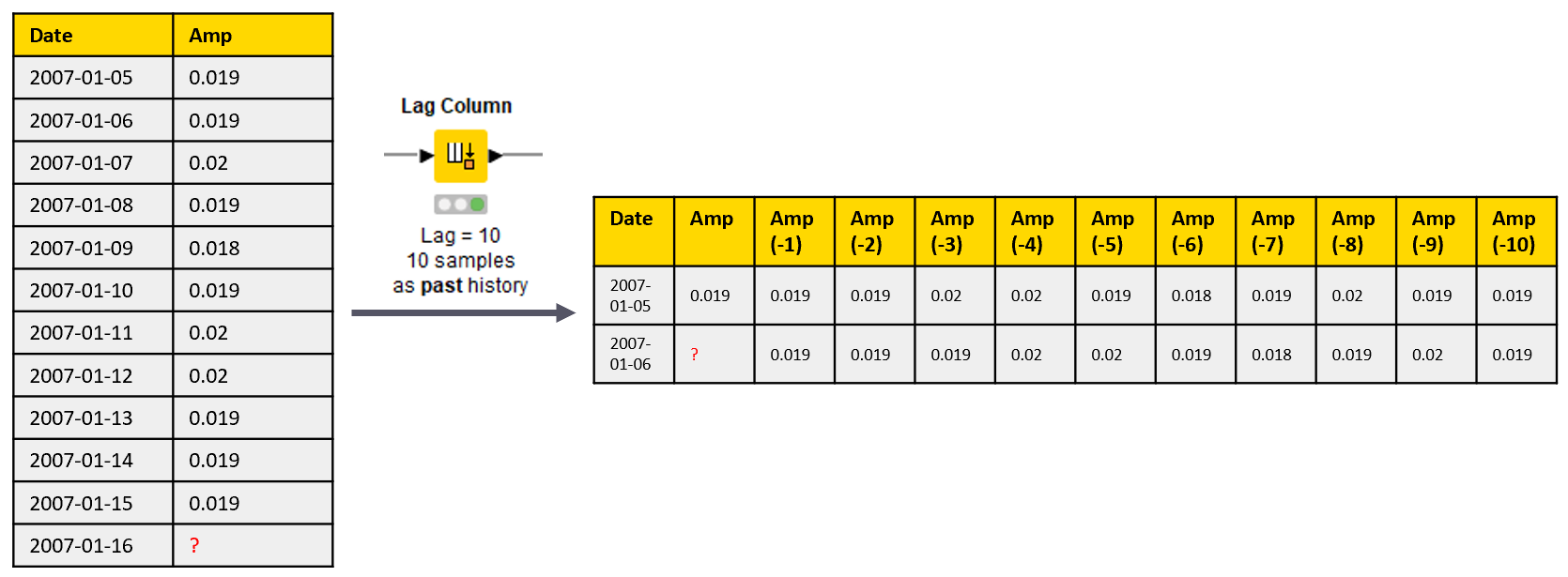
We train the models on the data from the training window. We loop over all 313 columns in the data representing the amplitude values on the single frequency bands. For each column at a time, we generate the predictor columns with the Lag Column node that puts the data in the p previous rows into p new columns. The transformed table contains the target column and a column for each past value at a different lag 1,2,...,p. These are the predictor columns of the auto-regressive model called xx (-1), xx (-2), …, xx (-p), where xx refers to the name of the target column and the number in the brackets refers to the lag (Figure 2).
Next, we train a linear regression model on the transformed data, and save the model as a PMML file. This model will be used later to predict the future values. We also perform in-sample prediction, that is we apply the model to the training data, and save the prediction error statistics. You can see this in the workflow in Figure 1, where the predictor node takes the same input data as the learner node.
Test the Model
Next, we want to know the out-sample prediction performance of our model, so we predict the data from the maintenance window. The model testing steps are shown in the Anomaly Detection. Time Series AR Testing workflow in Figure 3.
We loop over all 313 columns in the maintenance window and predict the values in it. We compare the predictions to the actual values and compare the prediction errors to the in-sample prediction errors. Finally, we calculate 1st and 2nd level alarms and visualize them.
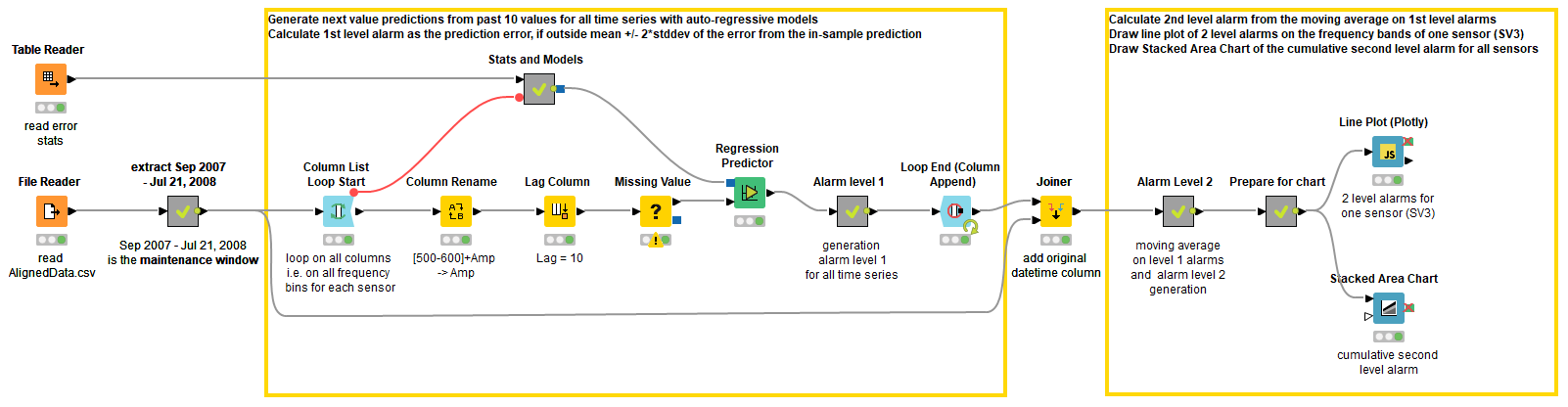
You can download the Anomaly Detection. Time Series AR Testing workflow on the KNIME Hub.
Calculate the 1st and 2nd level Alarms
The 1st level errors are calculated by comparing the in-sample prediction errors (on the training set) and out-sample prediction errors (on the maintenance set). We limit the boundaries for the normal behavior as average (avg) +/- 2*standard deviation (stddev) of the in-sample prediction errors. We use the expression below inside the Rule Engine node to only keep the prediction errors (pred.error) that exceed these boundaries and discard the others:
pred.error >avg+2*stddev OR pred.error <avg-2*stddev => pred.error
TRUE => 0
2nd level alarms are calculated as the average of the backward window of 21 1st level alarms, which we can do with the Moving Aggregation node. The backward window based moving average substitutes the last sample of the window with the average value of the previous samples in the same window (Figure 4).
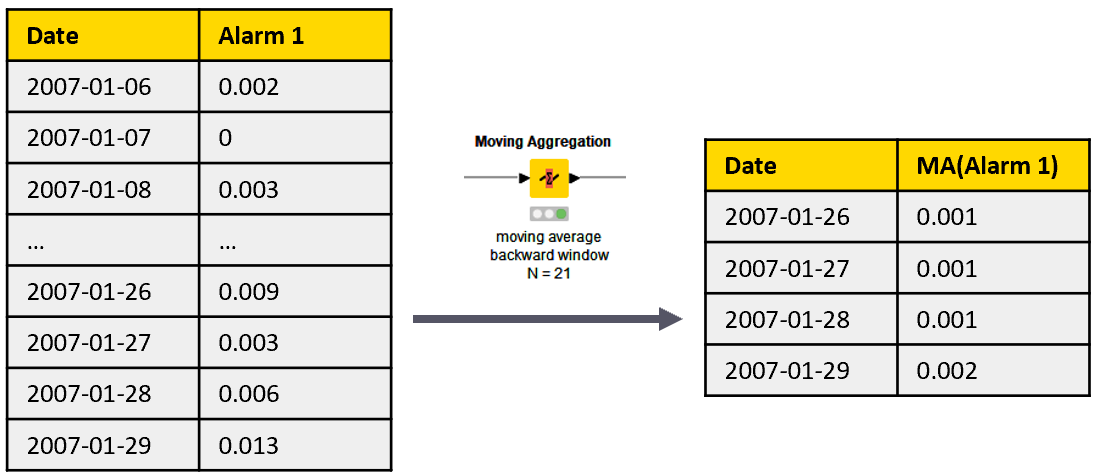
The backward window approach is necessary to simulate real life monitoring conditions, where past and current measures are available, but future measures are not. The moving average operation smooths out all random peaks in the 1st level alarm time series, and produces peaks in the 2nd level alarm time series, only if the 1st level alarm peaks persist over time.
Visualize Time Series with Line Plot and Stacked Area Chart
We observe the evolution of the 2nd level alarm time series before the rotor breakdown in a line plot and a stacked area chart.
Figure 5 shows a line plot with the 2nd level alarms on multiple frequency bands of one sensor (SV3) through the maintenance window from September 2007 to July 21, 2008. As you can see, in the first months of the maintenance window, hardly any alarms were raised. However, starting in May 2008, about 3 months before the rotor breakdown in July 21, 2008, the second level alarms were raised on all frequency bands. Especially the [200-300Hz] frequency band (the purple line) reacts strongly to the deteriorating rotor.
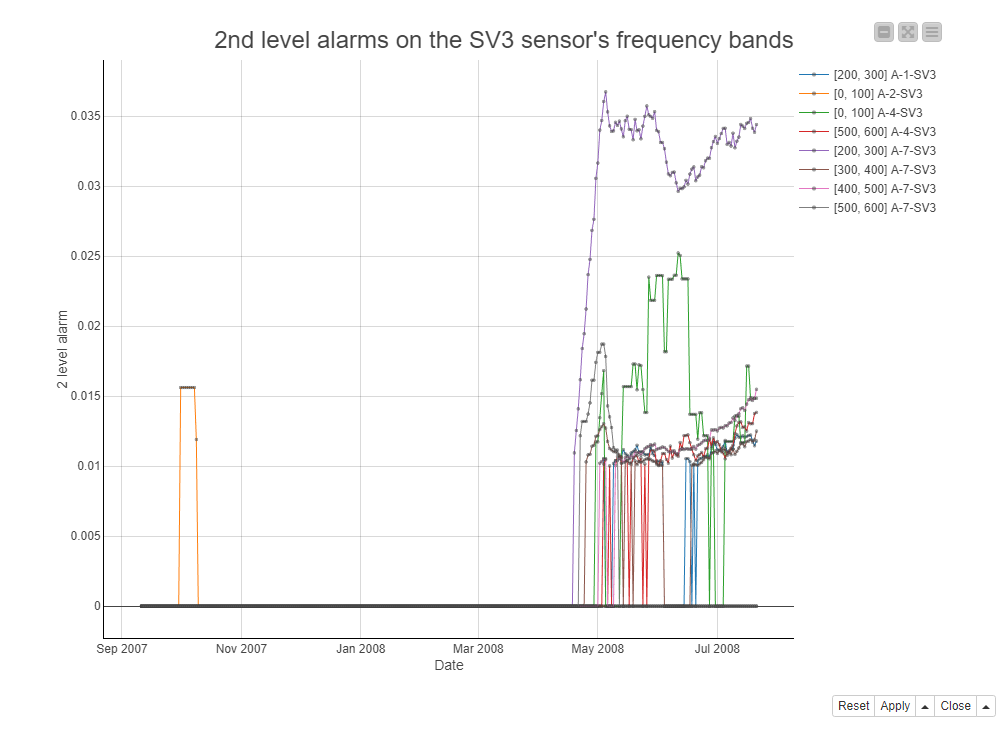
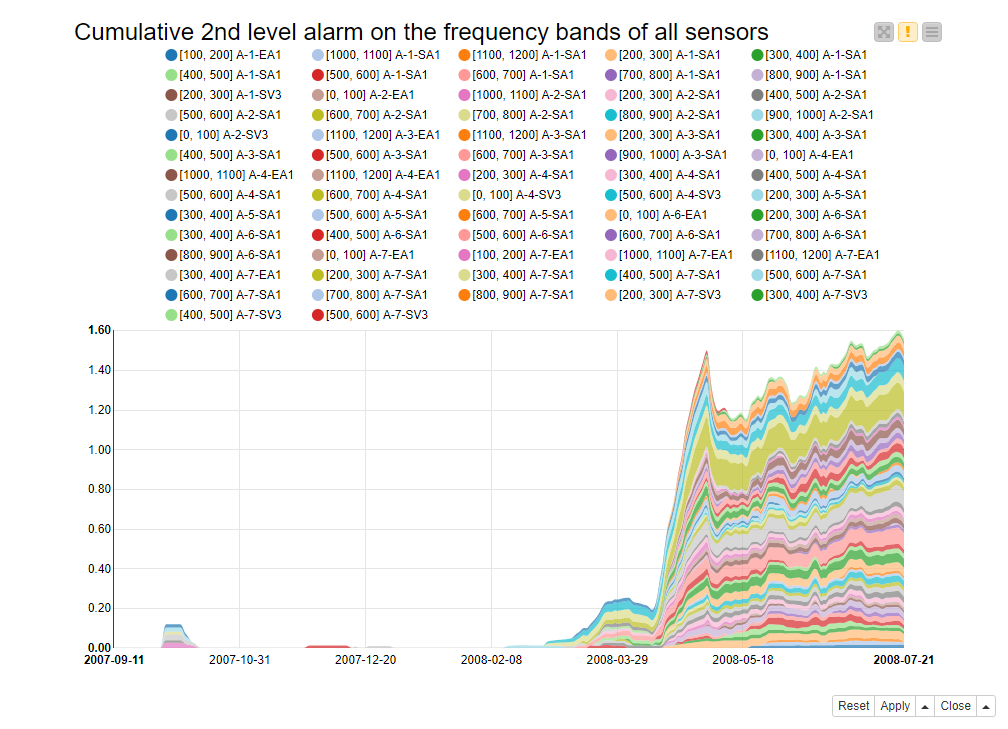
Figure 6 shows a stacked area chart with the cumulative 2nd level alarm across all frequency bands and all sensors through the maintenance window. Here the earliest signs of the rotor malfunctioning can be tracked back as early as the beginning of March 2008. However, the change in the system became evident at the beginning of May 2008, especially in some frequency bands of some sensors (see [200-300] A7-SA1 time series with a green area).
Considering the rotor breakdown on July 21, 2008, this would have been a fairly advanced warning time! If we wanted to have an earlier/later sign of the rotor malfunctioning, we could change the thresholds for the 1st and 2nd level alarms, and make them less/more tolerant towards prediction errors.
Take Urgent Action - Switch Off System via REST Service
We know now that our alarm system starts bugging us before the rotor breakdown. What should we do? We decided to notify the mechanical support via email. If it was more urgent, we could, for example, switch off the system immediately via a REST service.
We do this in the Anomaly Detection. Time Series AR Deployment workflow. The workflow is the same as the Anomaly Detection. Time Series AR Testing workflow shown in Figure 3, but it sends an email to the mechanical support if a 2nd level alarm is active and exceeds a threshold 0.1. This last part of the workflow is shown in Figure 7. The Call Workflow (Table based) node sends the input data to another workflow via REST, and collects the output of the workflow, if there’s any.

You can download the Anomaly Detection. Time Series AR Deployment workflow from the KNIME Hub.
The workflow we call is shown in Figure 8. The Send Email node - as the name says - sends an email using a specified account on an SMTP host and its credentials. The other node in the workflow is a Container Input (Variable) node. While this node is functionally not important, it is required to pass the data from the calling to the called workflow. Indeed, the Call Workflow (Table Based) node passes all the flow variables available at its input port to the Container Input (Variable) node. In summary, the Container Input (Variable) node is a bridge to transport the flow variables available at the caller node into the called workflow.
If we decided to, for example, switch off the system instead, we would only need to change the configuration of the Call Workflow (Table based) node to trigger the execution of such a workflow. Otherwise the deployment workflow would remain the same. Also notice that we triggered the execution of a local workflow from another local workflow. However, if we wrapped the workflow with the Container Input and Container Output nodes and deployed it to a KNIME Server, the workflow could be called from any external service.
Summary of Building Auto-Regressive Model to Predict Rotor Breakdown
In this article, we built an auto-regressive model to predict the rotor breakdown. We categorized single remarkable prediction errors as 1st level alarms, and persisting 1st level alarms as 2nd level alarms. We then tested the model on the maintenance window that ends in the rotor breakdown. In the deployment phase, we automatically sent an email for mechanical support if the 2nd level alarm was active.
We conclude the “Anomaly Detection in Predictive Maintenance” series here. We have explored three techniques: visual exploration, the control chart and lastly auto-regressive model. All techniques were able to detect the slowly changing patterns of sensor data as collective anomalies.
All associated workflows for Anomaly Detection in Predictive Maintenance are available in the 17_AnomalyDetection workflow group on the KNIME Hub.
