In todays blog post I want to explore some different approaches to dealing with missing values in data sets in the KNIME Anlaytics Platform. Missing data is a problem that most people have to deal with at some point, and there are different approaches to doing so.
Before proceeding, it is important to note that the missing data in this data set is Missing Completely At Random. The methods here are designed to work for this type of omission. If your data is Missing Not at Random, these methods may lead to systematic errors in your analysis.
For a more complete description of the types of missing data and a lot of other good information on the topic, can be found (as usual) in the associated Wikipedia article.
The example data I will work with is based on weather station data from San Francisco International Airport. This data set contains hourly temperature, wind speed, barometric pressure and precipitation levels for a 2 year period from 1993-1994.
In the first example workflow, shown in the following figure, we use the weather data, not including the time information, to try to build a predictive model for temperature, based on on the other measurements available from our weather station. Using a Regression Tree Ensemble, we are able to build a model with a root mean squared error of about 1.7 degrees C. This serves as a crude baseline to which we can compare our missing value treatment methods. For regression the KNIME node Tree Ensemble Learner (Regression) is used, requiring the extension "Decision Tree Ensembles" in KNIME Labs Extensions.
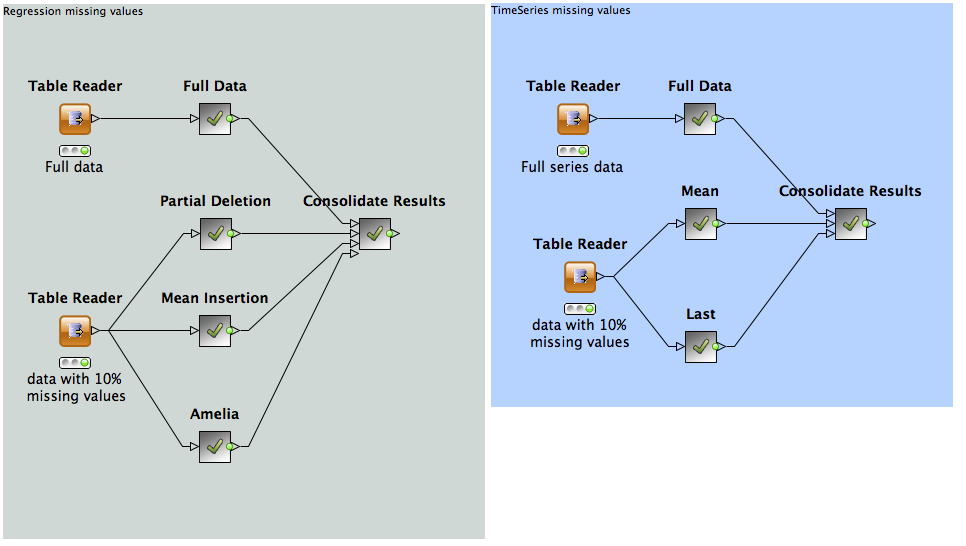
After randomly introducing 10% missing values in all of our predictors, we attempt 3 different methods to correct the data set prior to prediction:
- Partial Deletion - Here we remove all rows with missing values from our training set and then insert the mean values from each column into missing data from records to be predicted against.
- Mean insertion - rather than removing data from the training set, we introduce the mean value for the set in the hopes that our richer training data will outweigh the errors introduced from our estimation.
- Partial Imputation. Using the R package Amelia, Missing values are estimated "m" times. Models are constructed using the "m" completed data sets and then used for prediction as normal. To call R from within KNIME the nodes "R View" and "R Snippet" are used, requiring the extension "R Statistics Integration" in KNIME Extensions. Make sure that the package Amelia is installed in the R installation used by the KNIME - R Statistics Integration.
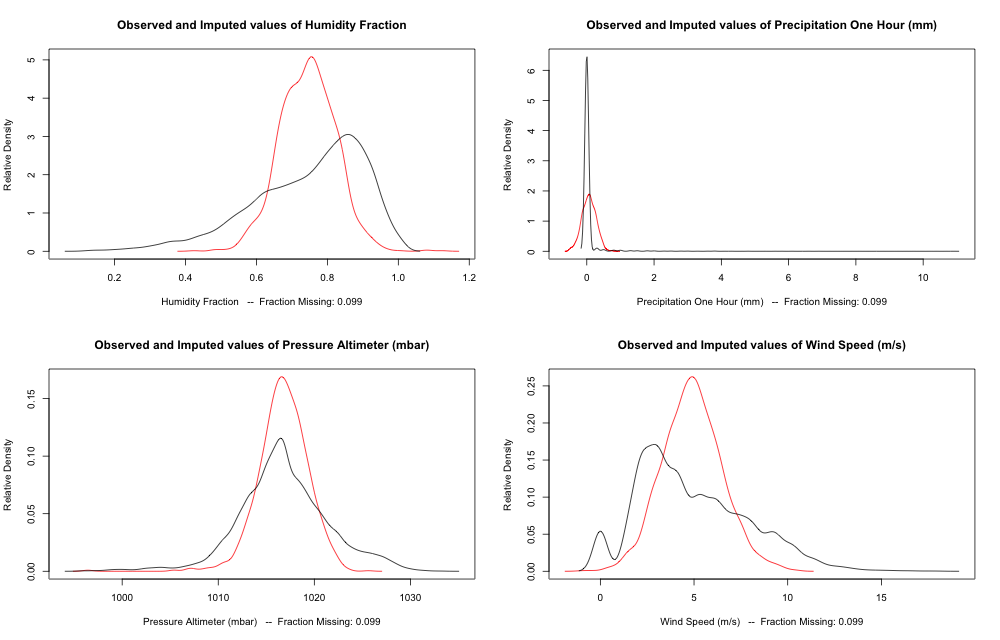
The distribution of estimated missing values (red) compared to existing data (black).
Results are shown in the figure above. Take these with a grain of salt, the results haven't been cross validated but they suggest that using the mean value as a place holder is better than dropping the record, but not as good as making a more rigorous imputation.
For our second example, we investigate how to deal with missing data when other variables are not available. For example, we may wish to build a forecasting system that can tell us the what the weather will be like tomorrow based on how it was in the past few days (using the Lag node in KNIME). In this case, our baseline with the full data will give us a root mean squared error of 2.2 Degrees.
Using approach 2 from above with the regular Missing Values node in KNIME gives us a result which is about 10% worse (RMSE=2.4%).
As it turns out though, this case is actually much easier to deal with than our other example as we may simply use the most recent known value as is available from the Time Series Missing Value node. This gives us a result similar to what we can achieve with the full data.
In the name of keeping this short, I'll stop here, but hopefully this post has gotten you to think about the best ways of dealing with missing values in your data.
The example workflow of this blog post can be downloaded here.
