Distance Measures in KNIME

With KNIME 2.10 new distance nodes have been released that allow the application of various distances measures in combination with the clustering nodes k-Medoids and Hierarchical Clustering, the Similarity Search node, and the Distance Matrix Pair Extractor node. Besides numerical distances such as p-norm distances (Euclidean, Manhattan, etc.), or cosine distance, also string distances, and byte and bit vector distances are provided. On top distances can be aggregated. If you still can't find the distance function you are looking for you can easily implement a customized distance with only one or two lines of Java code, using the Java Distance node. To get the nodes that make use of the new distances install the "KNIME Distance Matrix" extension (KNIME & Extensions -> KNIME Distance Matrix).

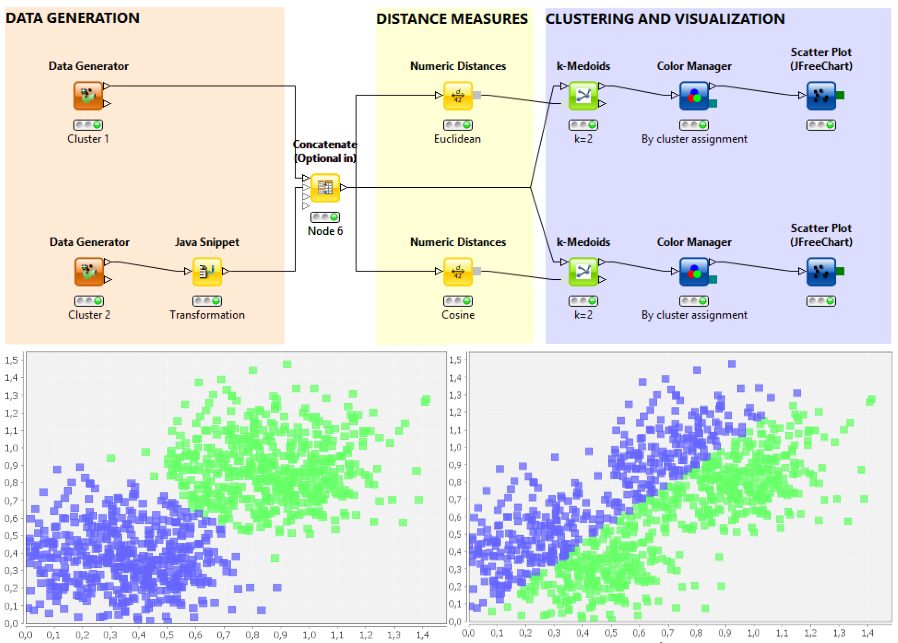
The following figure shows a KNIME workflow and two scatter plots. The workflow clusters data points with k-Medoids (k=2), using the Euclidean (left scatter plot) and cosine (right scatter plot) distance.

Many data mining algorithms use distance functions to determine the relationship between data points. A prominent example is the k-Nearest Neighbor, which determines the class of a pattern based on a (weighted) vote of the classes of its nearest neighbor in the training set, whereby the term 'nearest' is dependent on the selected distance function. A very similar aspect can be observed by many cluster algorithms such as the k-Means, k-Medoids or density based algorithms like DBSCAN: the distance function besides other parameters determines the result.

With Version 2.10 KNIME addresses this subject by providing the Distance Measure port. Encapsulating distance measures does not only reduce redundancy but may also lead to an enlargement of the possible input domain of certain nodes. The Distance Measure framework is easy extendible, so if a certain distance measurement is still missing, you are very welcome to contribute a custom distance. The developers guide shows the extension procedure in detail.

A distance measure in KNIME is a function

d : X × X → R

where X is a set of DataRows with the same schema. Applying the following additional conditions transforms the distance measure into a metric or distance function:

1. d(x, y) ≥ 0 (non-negativity, or separation axiom)
2. d(x, y) = 0 if and only if x = y (identity of indiscernibles, or coincidence axiom)
3. d(x, y) = d(y, x) (symmetry)
4. d(x, z) ≤ d(x, y) + d(y, z) (subadditivity / triangle inequality).

A distance measure can have the metric property, but this is not mandatory. However most algorithms expect at least some of the metric conditions to work correctly.

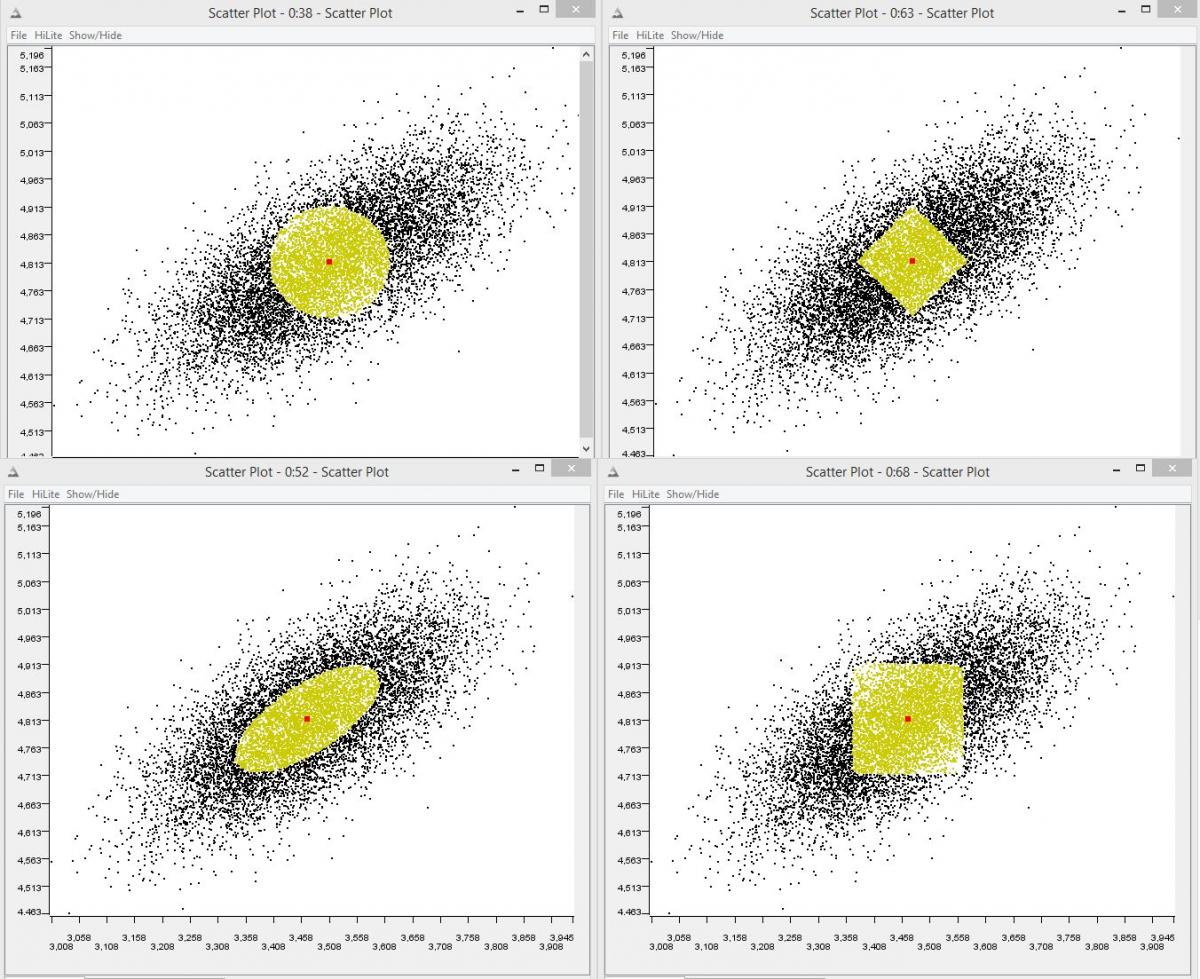
The choice of a distance measure influences fundamentally the result of distance based algorithms. The following figure illustrates this effect by a collection of common numerical distances. All points with a defined maximum distance d to the center point (red) are highlighted (yellow). As one can imagine a similarity search which should return all neighbors to the center with maximum distance d will obviously return a different result set.

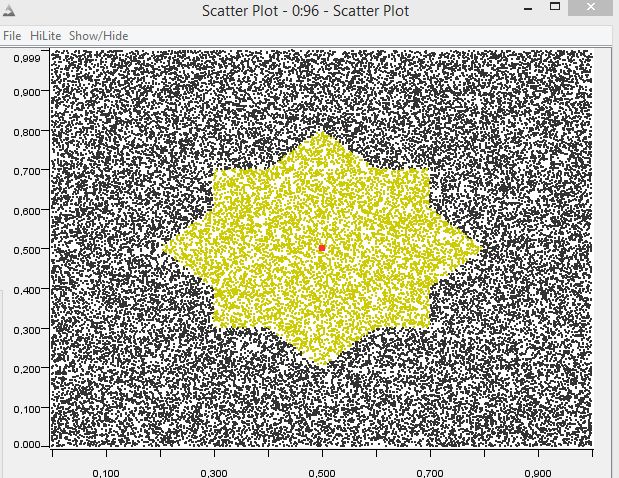
Another interesting point is to combine distances. The following figure shows a weighted combination of the Manhattan and Chebyshev (maximum) distance.

A distance measure is a new port (light grey) available at all nodes that support the distances. The usage is intuitive. Add the distance measure node of your choice to the workflow and connect the data input port to the data set. Connect the output port of that distance node to the distance input port of the node that is applying the distance. Additionally connect the same data set to the data input port of that node.

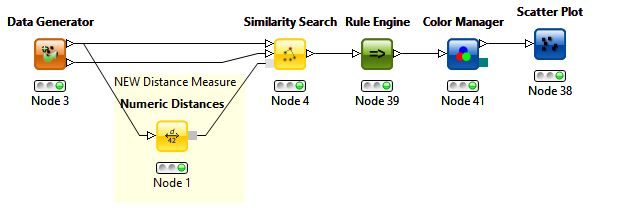
An example can be seen in the following figure. A numeric distance is applied on an artificially generated dataset. The output distance port of the Numeric Distance node is connected to the Similarity Search node, using that numeric distance. Additionally the same data set is connected to the first data input port of the Similarity Search node.

Overview of all nodes which have been changed or added with the Distance Measure framework in KNIME 2.10:

• Numerical Distances - Comprises numeric distances, like the Euclidean or Cosine distance
• String Distances - Set of string based distance measures, like the Levenshtein distance
• Bit Vector Distances - Typical Bit Vector distances, like the Tanimoto coefficient
• Byte Vector Distances - Contains distances optimized for Byte Vectors, like the Euclidean or Cosine distance
• Mahalanobis Distance - Measures the distance of two data sets with respect to the variance and covariance of the selected variables
• Matrix Distance - Wraps a pre-computed Distance Matrix in a distance measure. This is helpful if the distance measure is costly

• Java Distance - Allows to define a custom distance with a few lines of Java code
• Aggregated Distance - Combines two or three input distances to an aggregated distance

• Similarity Search
• Hierarchical Clustering (DistMatrix)
• Distance Matrix Calculate
• k-Medoid​​s

The KNIME workflow used to create the images is available for download in the attachment section of the blog. More workflows can be downloaded from the KNIME Example Server:

• knime://EXAMPLES/060_Webinars/Whats_New_in_2.10/2%20Data%20Mining%20-%20Distance%20Measures/Numeric%20Distances
• knime://EXAMPLES/060_Webinars/Whats_New_in_2.10/2%20Data%20Mining%20-%20Distance%20Measures/Address%20Deduplication

• Choropleth with R and KNIME
• Testing is fun!